UNIDAD # 5 (5.4)
Unidad # 5.4
💙5.4 POLIEDROS Y CUERPOS
REDONDOS💙
La geometría del
espacio estudia los cuerpos que tienen tres dimensiones: longitud, anchura y
altura.
👉Los cuerpos que tienen
sus caras planas se llaman poliedros.
👉Los cuerpos redondos
tienen alguna cara que es una superficie curva.
💥POLIEDROS💥
Aunque su forma sea muy
diferente, en todos los poliedros podemos observar algunos elementos comunes:
caras, vértices y aristas.
📌Caras son los
polígonos que forman su superficie.
📌Aristas
son segmentos, son los lados de las caras. Cada arista hace frontera de dos
caras.
📌Vértices son los puntos extremos de las aristas. En cada vértice concurren tres o más caras.
📌Vértices son los puntos extremos de las aristas. En cada vértice concurren tres o más caras.
💎Poliedros Regulares
Cuando todas las caras
de un poliedro son polígonos iguales y regulares decimos que el poliedro es
regular. Sólo hay 5 poliedros regulares: el tetraedro, el cubo, el octaedro, el
dodecaedro y el icosaedro.

💎Poliedros
Irregulares: Prismas
y pirámides
👉Los prismas son poliedros formados por dos
bases iguales y por caras laterales que son paralelogramos. Los prismas se
nombran por el polígono de sus bases.
Los prismas se nombran
según sea el polígono de sus bases: prisma triangular, cuadrangular,
pentagonal, hexagonal, etc.
👉Las pirámides son poliedros con una sola
base formada por un polígono cualquiera, y sus caras laterales son triángulos.
Las pirámides se nombran por el polígono de base.
Se nombran según sea el
polígono de su base: pirámide triangular, cuadrangular, pentagonal, hexagonal,
etc.
Son aquellos que
tienen, al menos, una de sus caras o superficies de forma curva. Esto les
permite diferenciarse de los cuerpos planos o poliedros, compuestos totalmente
por caras planas, también se denominan cuerpos de revolución porque pueden
obtenerse a partir de una figura que gira alrededor de un eje. Y estos son: el
cono, el cilindro y la esfera.
🌈CONO🌈
El cono es un cuerpo
geométrico generado por un triángulo rectángulo al girar en torno a uno de sus
catetos.
💦Elementos del cono
📍Eje: es el cateto AC.
Alrededor de él gira el triángulo rectángulo.
📍Base: es
el círculo que genera la rotación del otro cateto, AB. Por lo tanto AB es el
radio del cono. La base se simboliza: O (A, AB).
📍Generatriz: es
la hipotenusa del triángulo rectángulo, BC, que genera la región lateral
conocida como manto del cono.
📍Altura: corresponde
al eje del cono, porque une el centro del círculo con la cúspide siendo
perpendicular a la base.
El cono tiene una
cara basal plana y una cara lateral curva. Posee una arista basal y un vértice
llamado cúspide.
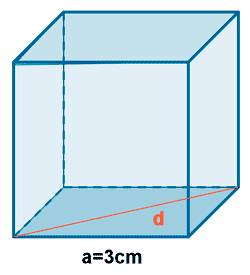
Hallar la diagonal de un cubo de 3 cm de arista.
🌈CILINDRO🌈
El cilindro es el
cuerpo geométrico generado por un rectángulo al girar en torno a uno de sus
lados.
✨Elementos del cilindro
💊Eje: lado
AD, alrededor del cual gira el rectángulo.
💊Bases: son los círculos paralelos y congruentes que se generan al girar los lados AB y CD del rectángulo. Cada uno de estos lados es el radio de su círculo y también, el radio del cilindro.
💊Altura: corresponde al mismo eje AD; es perpendicular a las bases y llega al centro de ellas. Esta es la razón por la que el cilindro es recto.
💊Bases: son los círculos paralelos y congruentes que se generan al girar los lados AB y CD del rectángulo. Cada uno de estos lados es el radio de su círculo y también, el radio del cilindro.
💊Altura: corresponde al mismo eje AD; es perpendicular a las bases y llega al centro de ellas. Esta es la razón por la que el cilindro es recto.
💊Generatriz: es
el lado BC, congruente con el lado AD, y que al girar forma la cara lateral o
manto del cilindro.
El cilindro tiene 2
caras basales planas, paralelas y congruentes. 1 cara lateral que es curva y 2
aristas basales.
🌈ESFERA🌈
La esfera es
el sólido generado al girar una semicircunferencia alrededor de su diámetro.
🌂Elementos de la esfera
Al girar el semicírculo alrededor del diámetro AB, se genera una superficie esférica donde se determinan los siguientes elementos:
Al girar el semicírculo alrededor del diámetro AB, se genera una superficie esférica donde se determinan los siguientes elementos:
🌠Generatriz: es
la semicircunferencia que genera la superficie esférica.
🌠Centro de la esfera: es el centro de la semicircunferencia y corresponde al punto O.
🌠Radio de la esfera: es el radio de la semicircunferencia: OA.
🌠Diámetro de la esfera: es el segmento que une 2 puntos opuestos de la superficie esférica, pasando por el centro: AB.
🌠Centro de la esfera: es el centro de la semicircunferencia y corresponde al punto O.
🌠Radio de la esfera: es el radio de la semicircunferencia: OA.
🌠Diámetro de la esfera: es el segmento que une 2 puntos opuestos de la superficie esférica, pasando por el centro: AB.
👉La esfera tiene una sola cara curva
Todos los puntos que forman la superficie esférica equidistan de uno fijo llamado centro, y que corresponde al centro de la semicircunferencia que gira.
Todos los puntos que forman la superficie esférica equidistan de uno fijo llamado centro, y que corresponde al centro de la semicircunferencia que gira.
👉Cortes👈
Una esfera puede ser cortada por un plano que pasa por su centro. De esta forma se obtienen 2 semiesferas y el plano deja como borde un círculo máximo.Si el plano corta a la esfera sin pasar por su centro se obtienen 2 casquetes esféricos.
Una esfera puede ser cortada por un plano que pasa por su centro. De esta forma se obtienen 2 semiesferas y el plano deja como borde un círculo máximo.Si el plano corta a la esfera sin pasar por su centro se obtienen 2 casquetes esféricos.
👉EJERCICIOS👈
💥Ejercicio 1:Hallar la diagonal de un cubo de 3 cm de arista.
💥Ejercicio 2:
Echamos
10 cm3 de agua en un recipiente cilíndrico de 2 cm de radio. ¿Qué altura alcanzará
el agua?
💥Ejercicio
3:
Calcular
el peso de una esfera maciza sabiendo que la densidad es de 8 kg/cm3 y cuyo
radio mide 4 cm.















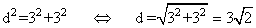











Comentarios
Publicar un comentario